| Modellbildung mit Videoanalyse - Hausarbeit von Jannis Weber |
 |
Bei der mathematischen
Modellbildung mittels Modellbildungsprogrammen geht es unter anderem
darum, dass Schüler selbständig Hypothesen über physikalische
Zusammenhänge entwickeln. Nachdem diese mathematische Modellbildung
abgeschlossen ist, wird der Ablauf vom Computer berechnet. Dieses wird
dann von den Schülern durch den Vergleich zwischen einerseits erwartetem
und anderseits simuliertem Verhalten bewertet oder verändert. Die Idee von
Modellbildungsprogrammen ist dabei, dem Benutzer die Berechnungen der
Bewegungsfunktionen abzunehmen und die in vielen Fällen zu anspruchsvolle
Mathematik unsichtbar in den Hintergrund zu legen. Hier bietet es sich an,
die berechneten Daten der mathematischen Modellbildung mit den Messdaten
der Videoanalyse zu vergleichen und so das Modell solange abzuändern, bis
es zu den Messdaten passt.
Herr Weber hat in seiner wissenschaftlichen
Hausarbeit „Kombination von
Videoanalyse und mathematischer Modellbildung“ Möglichkeiten
aufgezeigt, wie man Modellbildung und Videoanalyse verbinden kann.
Nach der Einleitung wird im zweiten Kapitel erläutert, was für den Einsatz von Videoanalyseprogrammen spricht. Dann wird dargelegt, auf was man beim Filmen von Videos achten soll. Schließlich wird ein kurzer Überblick über die drei Videoanalyseprogramme "measure dynamics", "Tracker" und "Coach 6 Studio MV" gegeben. Im dritten Kapitel wird erläutert, was für den Einsatz von Modellbildungsprogrammen spricht. Schließlich wird ein kurzer Überblick über die drei Modellbildungsprogramme "Newton-II", "Tracker" und "Coach 6 Studio MV" gegeben. Der Hauptteil der Hausarbeit ist das vierte Kapitel, in dem zwölf verschiedene Bewegungen gemessen, modelliert und verglichen werden (teils noch mit Varianten, so dass es 17 Modelle sind). Alle Experimente wurden mit allen drei Videoanalyseprogrammen analysiert und mit allen drei Modellbildungsprogrammen modelliert, um jeweils Erfahrungen zu sammeln und Vor- und Nachteile zu erkennen. Im fünften Kapitel werden kriteriengeleitet die verwendeten Programme anhand von sechs selbst gewählten Kriterien verglichen (Bedienung, Genauigkeit, Schnelligkeit, Darstellungsmöglichkeiten, Einstellungsmöglichkeiten, Preis/ Verfügbarkeit).
Nach dem Standardversuch der fallenden Kugel wird ein fallender Papierkegel untersucht. Ein Auto, bei dem der Teil des Fadens, der in der Luft hängt, durch eine den Boden erreichende Kette ersetzt wird, ist ein bekanntes Beispiel, bei dem sich die Masse ortsabhängig ändert. Der Versuch, bei dem der Teil des Fadens, der am Auto angebracht ist, durch eine um die Umlenkrolle reichende Kette ersetzt wird, ist eine neue Idee. Der Versuch mit dem Wagen, auf dem sich eine auslaufende Wasserflasche befindet (zeitabhängige Masse), ist sowohl experimentell als auch bzgl. der Modellierung eine Herausforderung. An zweidimensionalen Bewegungen werden zwei schiefe Würfe modelliert, eine Kugel ohne relevante Luftreibung und ein Da Cau-Ball mit erheblicher Luftreibung. An Schwingungen werden eine Federschwingung, die Schwingung einer Wassersäule im U-Rohr und ein Fadenpendel modelliert. Schließlich werden noch Fallbewegungen mit Stößen am Boden behandelt.
grüne Punkte sind Messwerte aus der Videoanalyse

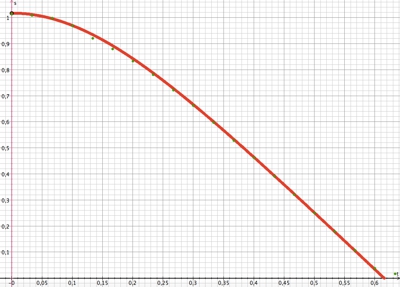
y(t)-Diagramm

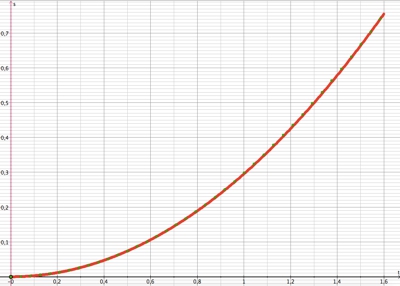
x(t)-Diagramm

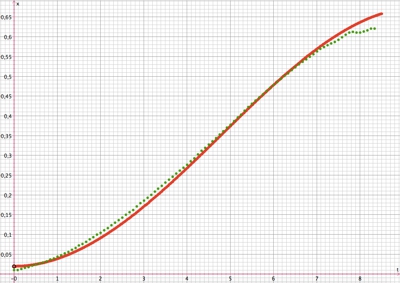
x(t)-Diagramm

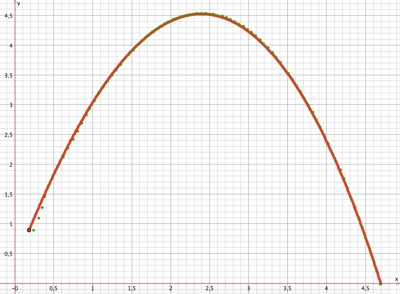
y(x)-Diagramm

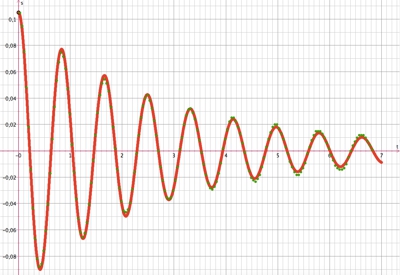
y(t)-Diagramm
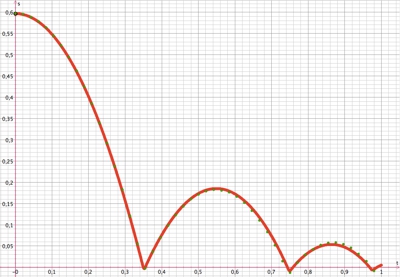
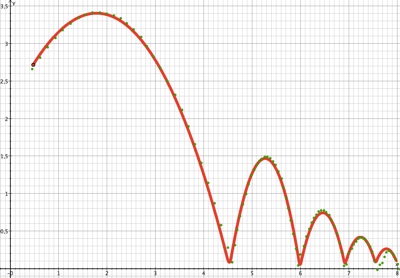
y(t)-Diagramm
y(x)-Diagramm
WEBER, J.; WILHELM, T.
Modellbildung und Videoanalyse
Plus
Lucis, Nr. 4, 2018, S. 18 - 25
[Download des gesamten Heftes als pdf]